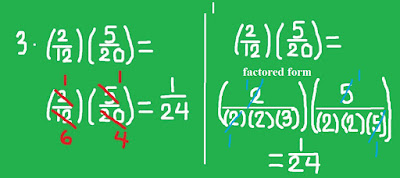how to multiply fraction and fraction, improper fraction, whole number, mixed numbers etc.

To multiply fraction and fraction


To multiply fraction and fraction

To multiply fraction and whole number

To multiply fraction and improper fraction

To multiply fraction and mixed number

To multiply 2 mixed numbers

contact us:    pepitodalupe@gmail.com

how to add fraction and whole number, improper fraction, mixed numbers

Addition of fraction and whole numbers
Examples:
1. 1/3 + 5 = 5 1/3
2. 4/6 + 12 = 12 4/6   or 12 2/3

Addition of fraction and improper fraction
Pre requisite : how to add fractions with different denominators
Examples:
1. 2/5 + 9/4 =

    2(4)  + 9 (5)   =
    5(4)      4(5)

      8   + 45       = 
      20    20     

        53    or 2 13/20
        20

2.    5/7 + 6/5 =

       5(5) + 6(7)  =
       7(5)    5(7)

         25   +  42    =
         35       35 

         67     or  1 32/35
         35



Addition of fraction and mixed numbers
Examples:
1. 4/9 + 3 1/4 =

     4/9 +  13/4                      3  1/4 = (4)(3)+1 =13/4   changed to improper fraction

      4(4)  + 13 (9) =
     9(4)        4(9)

      16     +   117  =
      36           36

      133    or  3 25/36
       36
Addition of mixed numbers and mixed numbers

2.  2 2/3  + 4 1/5  =       both mixed numbers

     8/3   +  21/5   =           changed to improper fractions

     8(5)   + 21(3)  =
     3(5)       5(3)

      40    +   63  =
      15         15

      103  or   6  13/15
       15  

contact us:    pepitodalupe@gmail.com

how to divide integers

To divide integers with like signs, divide the integers and quotient is always positive.

Examples:
1. (-20)/(-5) = 4      positive quotient
2. (100)/(10) = 10   positive quotient

To divide integers with unlike signs, the quotient is always negative

Examples:
1. (-36)/ (6) = -6   negative quotient
2. (81)/ (-9) = -9  negative quotient

contact us   pepitodalupe@gmail.com

how to find the common difference in arithmetic sequence

Pre requisite : how to add of integers, how to subtract  integers
To get the common difference in arithmetic sequence, subtract  the 2nd term to the first term, or  3rd term to 2nd term.....
Examples
1. 2, 4, 6, 8,....
    4 - 2 = 2      so the common difference is 2.. upon evaluating 6-(4), 8-(6), ....    will reveal
                        a common difference of 2 
6-(4)=
(6) +(-4) = 2

8-(6)=
8+(-6) =   2
                       knowing the common difference will give the discovery of succeeding pattern are
                        arithmetic sequence.
                       common difference is used in generating the next pattern as
                       2 + 2 = 4,  4+2 = 6,   6 + 2 = 8       so the arithmetic sequence is 2, 4, 6, 8 ......
                   

        

2. 12, 6, 0, -6, -12....
    (6)-(12) =
     (6) + (-12) = -6    so the common difference  is -6 upon evaluating 0 -(6), (-6)-(0), (-12)-(-6)...
                          will reveal a common difference of -6.
                          exposing....
     0 - (6)=
     0 +(-6)= -6    difference

     (-6)-(0) =
     (-6) + 0  = -6  difference

     (-12) - (-6)=
     (-12) + (6) = -6   difference     therefore the common difference is -6




Exercises:  Find the difference of the following arithmetic sequence.
1. 5, 10, 15, 20, .......
2. 3, 6 , 9, 12, .......
3. 100, 75, 50, 25, ....
4. 1/2, 1, 3/2, 4/2,.....
5. -4, -1, 2, .....
6. 3, 0, -3, -6, .....     







contact us     pepitodalupe@gmail.com
                          
   

how to multiply integers

To multiply integers with like signs, the multiply the factors and the product is always positive
 Examples
1. (-5) (-4) = 20
2. (9 ) (2)  = 18    
To multiply integers with unlike signs, the multiply the factors and the product is always negative.
Examples:
1. (-12) (2) = -24
2. (15) (-3) = -45

To multiply multiple products
Examples
1. (2) (-2) (1) = (-4) (1) = -4
2. ( -1) (1) (1) (-2) = (-1) (-2) = 2
3. (1) (2) (-3) (1) (-1) = (2)(-3) (-1) = (-6) (-1) = 6
                                   or
                                   =(2) (3) = 6

contact us pepitodalupe@gmail.com

The Odd and Even Numbers

     A  Math IQ test  was given to a 67  applicants of  AZ Security Agency . From the numbers 1, 2, 3, 4, 5, 6, up 100    identify the numbers that are  even and the odd numbers.
      
Name:________________                  Position Applied:_______________
                         
Part I                               Odd                                    Even
                          _______________                 ______________
                          _______________                 ______________
                         ________________                ______________

                        (100 pts.)

Part II   Why are  odd and even  words  appropriate  for its names?(Hint: count the
              letters )   (20 pts.)  

Part III   The total applicants are 67 , find sum of the given two digits? And  identify the sum if
               odd or even.  (20 pts.)
-------------------------------------------------------------------------------------------------------
The questions may become difficult if odd and even numbers could not be identified.


So odd numbers are whole numbers that are not divisible by 2 or can not  be divided exactly by 2
examples
1. 1, 3, 5, 7, 9, 11, ......
While even numbers are whole numbers that are divisible by 2 or can be divided by 2 exactly without remainder.
examples
2, 4, 6, 8, 10, 12,........ it is  multiple of 2

contact us pepitodalupe@gmail.com












     
                                  

how to subtract integers

to subtract the two integers , change the sign of the subtrahend and proceed to the law of addition of integers.
Examples
1. (-9) - (5)
    (-9) + (-5)  = -14    change the sign of the subtrahend integer and proceed to the law of
                                   addition of integers   ( see addition of integers with like signs)

2. (20) - (-45)
    (20) + (45)  =  65    change the sign of the subtrahend integer and proceed to the law of
                                   addition of integers   ( see addition of integers with like signs)     

3. (20) - (45)
    (20) +(-45)  =  -25 change the sign of the subtrahend integer and proceed to the law of
                                   addition of integers   ( see addition of integers with unlike signs)
4. (-55)- (-40)
    (-55) + (40)  = -15 change the sign of the subtrahend integer and proceed to the law of
                                   addition of integers   ( see addition of integers with like signs)
to be continued.....
contact us pepitodalupe@gmail.com

how to add of integers

Integers are  signed numbers which consists of positive numbers, negative numbers and zero.
To add integers it is grouped into two 1) addition of integers with the same signs  2)  addition of integers with unlike signs.

Addition integers with like signs
get the sum of the integers and affix the common sign
examples
1.   (-2) + (-12)  =   -14             the common of both integers is negative since -2 and -12 , upon
                                                  getting the sum or total affix the common which is negative before
                                                  the number.
2.     15  +  25    =  40                both numbers are positive so the common sign is positive.
                                                   if no sign is indicated in the answer it's positive.
3.     (-5)  + (-4)  + (-7) =   -16   getting the sum of integers the affix the common sign which is
                                                   negative before the number.

Addition of integers with unlike signs
Subtract from highest integer absolute value to the smaller integer absolute value and affix the sign
of integer with greatest absolute value to the answer.

Examples:
1. (-12) +  9    =    -3              the absolute value  /-12/ = 12   while /9/= 9   so 12- 9 = 3 then affix
                                               the sign of higher integer absolute value to the answer


2.  20 +  (-15) =   5                 the absolute value of /20/ = 20 while /-15/ = 15 so 20-15 = 5  then
                                                affix sign of  higher integer absolute value to the answer.

Visual examples:





1. (-4) + (-6 )    two groups of negative hexagons
                          combined together indicated by plus sign

 

                                                                      
  the negative pentagon                                                 arranging for easy counting,

   into one group                                                           the sum of negative pentagon is -10

 



2.  5 + 3                  the two groups of positive stars

                                to be combined together 


        

     grouping together                                                        arranging and counting, 8 positive stars

                                                                            






        3.    4 + (-5)     4 green positive chips combined with 5 yellow
                                 negative chips

                                       

arranging and eliminating pairs of positive and negative chips
so the remaining chips is only one  negative yellow.

in real life situation it may be a group of singles, then married
so eliminated to singleness. the only remaining single is one
female  if + is male .

                                                      if yellow chips are amount to be paid with + signs. the remaining
                                                      one negative. so still in debt for one chip.
to be continued....
contact us   pepitodalupe@gmail.com

How to add fractions with different denominators

In adding fractions with different denominators, find the least common multiple  of the fractions. That will then be the common denominator of the fractions. Then follow the steps of adding fractions with common denominator.

Examples:
1. 1/2 + 3/5         the denominator 2 and 5 are prime numbers so multiplying both equals to 10 as the
                             common denominator
                            following the least common multiple
                             2 = 2, 4, 6, 8, 10, 12,..........
                             5 = 10, 20, 30,.................        
                             with this multiples revealed that 10 is the least common multiple, therefore it will
                             then be the  common denominator of the fractions

   (1)(5)  + (3)(2)   =  To get  a denominator of 10, multiply (2)(5) in its denominator, multiply  also
   (2)(5)     (5)(2)         5 in its numerator so (1)(5) . Actually multiplying 5/5  to the fraction
                                    1/2 will just be renamed to 5/10 which is just same  as the                                
                                     original fraction 1/2 .
                                     In the fraction 3/5, multiply (3)(2) in its numerator and (5)(2) in its  
                                     denominator.
  5    +   6     =    11      adding both fraction with common denominator , the answer is 11/10
 10       10          10

2. 4/15 + 3/5                 the denominators are 15 and 5 ,getting the prime factors  provide us this table
                                      15 =      3 x  5
                                        5 = 1       x 5
                                               1 x 3 x 5 = 15   indicates as its  least common  denominator
                                     following the least common multiple
                                     15 = 15, 30, 45.......
                                       5=     5,   10,  15,  20, .....      LCM is 15     as the least common
                                                                                     denominator of the fractions
  4  +  (3)(3)  =
 15     (5)(3)                    4/15 is not changed because it holds the common denominator, so only 3/5
                                        is renamed as the denominator 5 multiplied by 3  will now be 15 .
 4    +   9      =    13          numerator must also be multiplied by 3  . multiplying a fraction of
15       15           15           3/3 is just equal to 1. So 3/5 =9/5.  The answer to the problem is 13/15





to be continued......
contact us    pepitodalupe@gmail.com

How to add and subtract fractions with the common denominator

The   addition of fractions with the same denominator is so easy to perform, just add their numerators and affix their common denominator.

Examples:
1.  1/2 + 1/2     =  2/2 or 1
2.  3/7 + 2/7     =  5/7
3.  8/15 + 5/15 = 13/15
4.  25/60 + 20/ 60 = 45/60 to reduce to simplest form give the prime factors
                                           so    45=      (3)(3)(5)    
                                                   60= (2)(2)(3) (5) 
                                           shaded yellow were eliminated,  answer is 3/4 

The subtraction of fractions with the same denominator or common denominator, just subtract the numerators and affix the common denominator

Examples
1.  5/6 - 2/6 = 3/6 or 1/2    why?   their prime factors are the following, shaded yellow removed.
                                                      3 = (1)(3)        
                                                      6 = (2)(3) 
                                                     the answer is 1/2
2. 4/5 - 2/5 = 2/5
3. 12/35- 10/35 = 2/35
4. 8/50 - 7/50 = 1/50
5. 9/17 - 4/17 = 5/17  

contact us: pepitodalupe@gmail.com